Photo by Enric Moreu on Unsplash

A few weeks ago, I came across this interesting paper, Parsing Gigabytes of JSON per Second. 2.5 Gigabytes of JSON per second on commodity processors, to be precise. Three pages into the paper, I discovered that I needed more background knowledge on SIMD instructions. SIMD is like the Mona Lisa, I have an idea of what it looks like, but that representation is far from the actual painting. After reading a few articles and numerous build errors later, I’m confident enough to write on the topic.

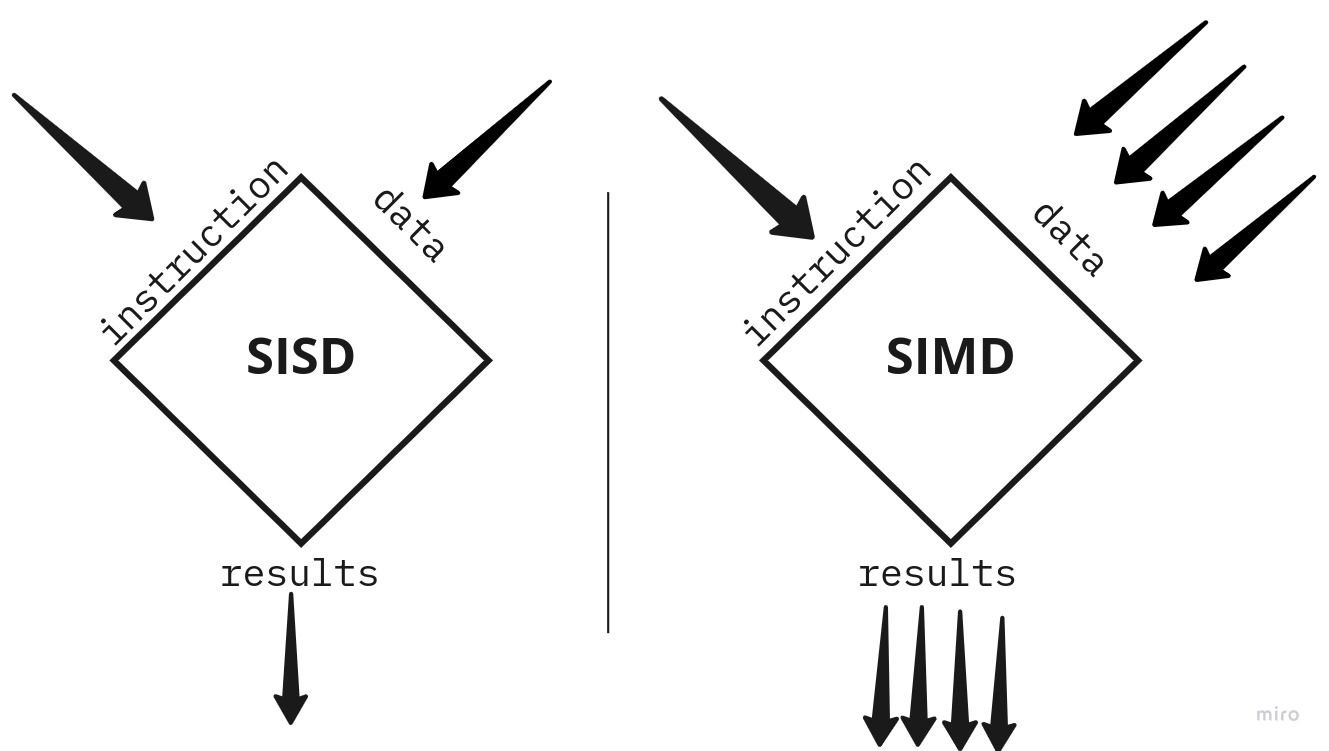
SIMD, short for Single Instruction Multiple Data, is a parallel processing model that applies a single operation to multiple sets of vectors. If you’re not familiar with SIMD, there are several great introductory articles and slides on the topic.

the setup

I chose to benchmark the dot product operation because it’s a cheap operation, constrained only by the input size. The input consists of two float vectors, a and b, each of size n.

Where a and b are vectors, n is the size of the vectors, and ai & bi are vector components belonging to vectors a & b.

// Representation in pseudocode
number function dot_product(a[], b[], n) {
  sum = 0;
  for (i = 0; i <= n; i++) {
    sum = a[i] + b[i];
  }
  return sum;
}

The input size is computed as n x float size (bytes) x number of vectors (2). To avoid memory shortage, I capped the input size at 256 MB (two 128 MB vectors).

I ran all my benchmarks on a Quad core Intel Core i7-8550U CPU with a 1MB L2 cache and an 8MB L3 cache. This CPU supports AVX2.

implementation

I started by comparing two functions, a scalar implementation, and a vectorized implementation.

The first implementation matches the pseudocode example above. A loop that runs n times, adding the result of a[i] x b[i] to the variable sum.

The vectorized implementation follows the same pattern but has several key differences. Firstly, all the key variables are type __m256, a data type representing a 256-bit SIMD register. In simple terms, this is a vector of eight 32-bit floating-point values.

The loop count increments by eight because the function _mm256_loadu_ps (L21, L22) loads eight floating-point values from unaligned memory into a __m256 vector. The function _mm256_fmadd_ps multiplies matching elements from the first two vectors and adds them to the value in the matching index of the third vector. To ensure correct computations, I added an assert on L16 to ensure the input arrays size is a multiple of 8.

The function _mm256_storeu_ps moves eight floating-point values from a __m256 vector to an unaligned memory location.

compare results

I used google/benchmark to run my benchmarks.

Benchmark                            Time  CPU  Time Old  Time New  CPU Old  CPU New
-----------------------------------------------------------------------------------
[dot_product vs. dot_product_256]/1  -0.8158  -0.8158  155357  28624  155354  28623
[dot_product vs. dot_product_256]/2  -0.8117  -0.8117  302681  56987  302667  56987
[dot_product vs. dot_product_256]/4  -0.8004  -0.8004  595212  118786  595200  118786
[dot_product vs. dot_product_256]/8  -0.7486  -0.7486  1260476  316823  1260469  316824
[dot_product vs. dot_product_256]/16  -0.6466  -0.6466  2711183  958018  2711140  957993
[dot_product vs. dot_product_256]/32  -0.6019  -0.6019  5450561  2169969  5450430  2169929
[dot_product vs. dot_product_256]/64  -0.5795  -0.5795  11411248  4797997  11411161  4797871
[dot_product vs. dot_product_256]/128  -0.5781  -0.5781  23172851  9776048  23172549  9775924
[dot_product vs. dot_product_256]/256  -0.5554  -0.5554  44252652  19673917  44251304  19673560

Each row represents a comparison between dot_product and dot_product_256 with different input sizes. The values in Time and CPU columns are calculated as (new - old) / |old| (x 100 to get percentage). The last four columns are time measurements in nanoseconds.

I expected dot_product_256 to be faster, but I did not anticipate the big gap. 81.58% faster with an input size of 1MB, 55.54% faster with an input size of 256MB.

analysis I

You can view the full analysis on Compiler Explorer.

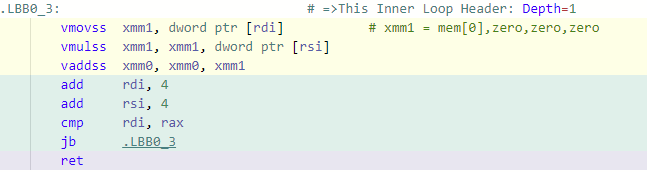
The scalar implementation has three AVX instructions corresponding to the loop statement sum += a[0] * b[0];:

• vmovss unloads the pointer value a[0] into a 128 bit register.
• vmulss multiplies the value a[0] with the value at pointer reference b[0].
• vaddss adds the result from the multiplication operation above to sum.

Compare that with the vectorized implementation instructions:

• vmovups loads eight floating-point values from a into a SIMD register.
• vfmadd231ps multiplies the eight floating-point values loaded from a with eight floating-point values loaded from b and adds the result to sum.

The xmm0-xmm7 registers used in the scalar implementations are 128 bit wide. In contrast, the vectorized implementation uses ymm0-ymm7 registers, which are 256 bit wide. The letters FMA in vfmadd231ps stand for Fused Multiply-Add, the technical term for the floating-point operation of multiplication and addition in one step.

compiler optimization

Up until this point, I’ve been using conservative optimization compiler flags -O3 and -march=native. I wanted to test another flag -ffast-math, which tells the compiler to perform more aggressive floating-point optimizations. Very similar to cutting the brakes on your car to make it go faster.

Benchmark                            Time  CPU  Time Old  Time New  CPU Old  CPU New
-----------------------------------------------------------------------------------
[dot_product vs. dot_product_256]/1  -0.0500  -0.0500  25535  24258  25535  24257
[dot_product vs. dot_product_256]/2  -0.0556  -0.0556  51505  48644  51504  48642
[dot_product vs. dot_product_256]/4  -0.0546  -0.0546  105722  99951  105718  99949
[dot_product vs. dot_product_256]/8  -0.1465  -0.1465  385659  329162  385646  329135
[dot_product vs. dot_product_256]/16 +0.0208 +0.0208  949516  969264  949485  969199
[dot_product vs. dot_product_256]/32  -0.0118  -0.0118  2301268  2274091  2301235  2274021
[dot_product vs. dot_product_256]/64  +0.0037  +0.0037  4863097  4881084  4862852  4880919
[dot_product vs. dot_product_256]/128  +0.0220  +0.0220  9883521  10101137  9883309  10101054
[dot_product vs. dot_product_256]/256  +0.0273  +0.0273  19079586  19601290  19079604  19600141

Both functions benchmark at almost equal speeds. dot_product_256 has the biggest lead, 14.65% (input size, 8 MB). dot_product is 2.73% faster on the largest input size, 256 MB.

analysis II

You can view the full analysis on Compiler Explorer

The scalar implementation compiled looks very different. The loop statement sum += a[0] * b[0]; now has 29 corresponding Assembly instructions. The compiler applied loop unrolling, an optimization strategy that minimizes the cost of loop overhead. The loop unrolls in four iterations. By examining one iteration, you’ll notice the use of 256 bit registers and SIMD intrinsics.

# First iteration: L33 - L40
vmovups ymm4, ymmword ptr [rsi + 4*rdx]
vmovups ymm5, ymmword ptr [rsi + 4*rdx + 32]
vmovups ymm6, ymmword ptr [rsi + 4*rdx + 64]
vmovups ymm7, ymmword ptr [rsi + 4*rdx + 96]
vfmadd132ps   ymm4, ymm0, ymmword ptr [rdi + 4*rdx] # ymm4 = (ymm4 * mem) + ymm0
vfmadd132ps   ymm5, ymm1, ymmword ptr [rdi + 4*rdx + 32] # ymm5 = (ymm5 * mem) + ymm1
vfmadd132ps   ymm6, ymm2, ymmword ptr [rdi + 4*rdx + 64] # ymm6 = (ymm6 * mem) + ymm2
vfmadd132ps   ymm7, ymm3, ymmword ptr [rdi + 4*rdx + 96] # ymm7 = (ymm7 * mem) + ymm3

Conclusion

Thanks to compiler optimization, the scalar implementation matches the vector implementation performance-wise. Both cases use SIMD registers and intrinsics, whether intentionally written or optimized later by the compiler. The optimized implementations handle larger data sets faster, but they have limits too.

Hardware, specifically the CPU, is the determining factor when optimizing with SIMD. Most modern CPUs support AVX2, fewer support AVX2-512 (512 bit wide registers).